飞飞侠

Time Limit: 50 Sec Memory Limit: 259 MB

Description

飞飞国是一个传说中的国度，国家的居民叫做飞飞侠。飞飞国是一个N×M的矩形方阵，每个格子代表一个街区。然

而飞飞国是没有交通工具的。飞飞侠完全靠地面的弹射装置来移动。每个街区都装有弹射装置。使用弹射装置是需

要支付一定费用的。而且每个弹射装置都有自己的弹射能力。我们设第i行第j列的弹射装置有Aij的费用和Bij的弹

射能力。并规定有相邻边的格子间距离是1。那么，任何飞飞侠都只需要在(i,j)支付Aij的费用就可以任意选择弹

到距离不超过Bij的位置了。如下图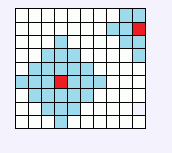

（从红色街区交费以后可以跳到周围的任意蓝色街区。）现在的问题很简单。有三个飞飞侠，分别叫做X，Y，Z。

现在它们决定聚在一起玩，于是想往其中一人的位置集合。告诉你3个飞飞侠的坐标，求往哪里集合大家需要花的

费用总和最低。

Input

输入的第一行包含两个整数N和M，分别表示行数和列数。

接下来是2个N×M的自然数矩阵，为Aij和Bij

最后一行六个数，分别代表X，Y，Z所在地的行号和列号。

1<=N,M<=150;0<=Aij<=10^9;0<=Bij<=1000

Output

第一行输出一个字符X、Y或者Z。表示最优集合地点。

第二行输出一个整数，表示最小费用。如果无法集合，只输出一行NO

Sample Input

4 4

0 0 0 0

1 2 2 0

0 2 2 1

0 0 0 0

5 5 5 5

5 5 5 5

5 5 5 5

5 5 5 5

2 1 3 4 2 2

Sample Output

Z

这道题还是很不错的。。。。

分层分成300层贼秀。。。。

但是我可能把 maxn >> 1 当成乘2了。。。

网上前两个std都是wa的。。。我拍了一万年。。。。

傻逼的我最后终于gou过去了。。。

#include
    
     using namespace std;const int maxn = 155;const long long INF = 2e16 + 5;struct lpl{    int i, j, k; long long dis;    bool operator < (const lpl &A)const{        return dis > A.dis;    }}node[maxn][maxn][maxn >> 1], lin, qwe;int n, m, maxh, sz, pn[5], pm[5], pa[] = {-1, 0, 1, 0, 0}, pb[] = {0, 1, 0, -1, 0};int A[maxn][maxn], B[maxn][maxn];long long ans, dis[maxn][maxn][maxn << 1], p[5][5];bool vis[maxn][maxn][maxn << 1];priority_queue
     
       q;inline int read() {    char ch = getchar(); int x = 0, f = 1;    while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}     while('0' <= ch && ch <= '9') {x = x * 10 + ch - '0'; ch = getchar();}    return x * f;}inline bool check(int i, int j){return (i >= 1 && i <= n && j >= 1 && j <= m);}inline void putit(){    n = read(); m = read(); sz = n * m;     for(int i = 1; i <= n; ++i)        for(int j = 1; j <= m; ++j){             A[i][j] = read(); A[i][j] = min(A[i][j], max(i - 1, n - i) + max(j - 1, m - j));            maxh = max(maxh, A[i][j]);                  }    for(int i = 1; i <= n; ++i)        for(int j = 1; j <= m; ++j)            B[i][j] = read();    for(int i = 1; i <= 3; ++i) pn[i] = read(), pm[i] = read();}inline void dijkstra(int a, int b){    int ii, jj, kk; memset(vis, false, sizeof(vis));    for(int i = 1; i <= n; ++i)        for(int j = 1; j <= m; ++j)            for(int k = 0; k <= 300; ++k)                dis[i][j][k] = 2e16;    ans = dis[1][1][1];    node[a][b][0].i = a; node[a][b][0].j = b; node[a][b][0].k = 0;     node[a][b][0].dis = 0; dis[a][b][0] = 0; q.push(node[a][b][0]);    while(!q.empty()){        lin = q.top(); q.pop(); ii = lin.i; jj = lin.j; kk = lin.k;        if(vis[ii][jj][kk]) continue;         if(vis[pn[1]][pm[1]][0] && vis[pn[2]][pm[2]][0] && vis[pn[3]][pm[3]][0]) break;        vis[ii][jj][kk] = true;        if(dis[ii][jj][A[ii][jj]] > lin.dis + B[ii][jj]){            dis[ii][jj][A[ii][jj]] = lin.dis + B[ii][jj];            qwe = lin; qwe.k = A[ii][jj]; qwe.dis = lin.dis + B[ii][jj];            q.push(qwe);        }        if(!lin.k) continue; kk = lin.k - 1;        for(int w = 0; w <= 4; ++w){            if(!check(lin.i + pa[w], lin.j + pb[w])) continue;            ii = lin.i + pa[w]; jj = lin.j + pb[w];            if(dis[ii][jj][kk] > lin.dis){                dis[ii][jj][kk] = lin.dis;                qwe.i = ii; qwe.j = jj; qwe.k = kk; qwe.dis = lin.dis;                q.push(qwe);            }        }    }    while(!q.empty()) q.pop();}int main(){    putit();    dijkstra(pn[1], pm[1]);     p[1][2] = dis[pn[2]][pm[2]][0]; p[1][3] = dis[pn[3]][pm[3]][0];    dijkstra(pn[2], pm[2]);     p[2][1] = dis[pn[1]][pm[1]][0]; p[2][3] = dis[pn[3]][pm[3]][0];    dijkstra(pn[3], pm[3]);    p[3][1] = dis[pn[1]][pm[1]][0]; p[3][2] = dis[pn[2]][pm[2]][0];    char t = 'Q';     if(p[2][1] + p[3][1] < ans){        ans = p[2][1] + p[3][1]; t = 'X';    }    if(p[1][2] + p[3][2] < ans){        ans = p[1][2] + p[3][2]; t = 'Y';    }    if(p[1][3] + p[2][3] < ans){        ans = p[1][3] + p[2][3]; t = 'Z';    }    if(t == 'Q'){printf("NO"); return 0;}    cout << t << endl << ans;    return 0;}